Objetivos
- Conocer y entender los conectivos lógicos
- Conocer y entender las tablas de verdad
- Aplicar las propiedades y resultados de los conectivos lógicos para resolver problemas
Proposiciones simples y compuestas
Recordamos que una proposición es una oración declarativa a la cual se le puede asociar un valor de verdad.Para representar proposiciones usaremos las letras p, q, r,...
Por ejemplo
q = hace frío
Así como en álgebra las variables que representan cantidades pueden formar expresiones más complejas mediante el uso de las operaciones básicas de aritmética y algunas funciones, en lógica podemos relacionar proposiciones mediante los conectivos lógicos.
Los conectivos lógicos son símbolos usados para combinar proposiciones simples dadas, produciendo así otras llamadas proposiciones compuestas.
Los conectivos lógicos que usaremos son
- ~ negación
 disyunción
disyunción conjunción
conjunción condicionante
condicionante bicondicionante
bicondicionante
Tablas de Verdad.
Definimos una tabla de verdad como un arreglo que nos permite tener los posibles valores de verdad de una proposición compuesta a partir de los valores de verdad de las proposiciones simples.Las tablas de verdad para los conectivos lógicos listados arriba son las siguientes:
Negación
La negación de una proposición es una nueva proposición que tiene un valor de verdad opuesto a la proposición original. Es decir, si el valor de verdad de una proposición p es verdadero, entonces el valor de verdad de ~p es falso.
La tabla de verdad para el conectivo ~ está dada por
| p | ~p |
|---|---|
| V | |
| F |
La disyunción es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo
 .
.Esta proposición compuesta de denota por
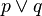 y se lee p o q.
y se lee p o q.La tabla de verdad para el conectivo
 está dada por
está dada por| p | q | 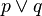 |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
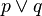 tenga valor de verdad verdadero, basta con una de las proposiciones simples tenga valor de verdad verdadero.
tenga valor de verdad verdadero, basta con una de las proposiciones simples tenga valor de verdad verdadero.Conjunción
La conjunción es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo
 .
.Esta proposición compuesta de denota por
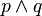 y se lee p y q.
y se lee p y q.La tabla de verdad para el conectivo
 está dada por
está dada por| p | q | 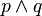 |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
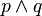 tenga valor de verdad verdadero, ambas proposiciones simples deben tener valor de verdad verdadero.
tenga valor de verdad verdadero, ambas proposiciones simples deben tener valor de verdad verdadero.Condicionante
La condicional es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo
 .
.Esta proposición compuesta de denota por
 y se lee p implica q.
y se lee p implica q.En esta proposición compuesta, la proposición simple p se llama antecedente, mientras que la proposición simple q se llama consecuente.
La tabla de verdad para el conectivo
 está dada por
está dada por| p | q |  |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
 tiene valor de verdad falso solamente cuando el antecedente es verdadero y el consecuente es falso. En cualquier otro caso, el valor de verdad de la proposición compuesta es verdadero.
tiene valor de verdad falso solamente cuando el antecedente es verdadero y el consecuente es falso. En cualquier otro caso, el valor de verdad de la proposición compuesta es verdadero.Bicondicionante
La bicondicional es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo
 .
.Esta proposición compuesta se denota por
 y se lee p si y solo si q.
y se lee p si y solo si q.La tabla de verdad para el conectivo
 está dada por
está dada por| p | q |  |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
 tiene valor de verdad verdadero siempre que las proposiciones simples tienen el mismo valor de verdad. Es cualquier otro caso, la proposición compuesta tiene valor de verdad falso.
tiene valor de verdad verdadero siempre que las proposiciones simples tienen el mismo valor de verdad. Es cualquier otro caso, la proposición compuesta tiene valor de verdad falso.Las proposiciones compuestas pueden combinarse o conectarse para formar proposiciones aún más complejas. Es claro que el valor de verdad de una proposición, por compleja que sea, depende de los valores de verdad de las proposiciones que las componen en sus formas más simples.
Para hacer la tabla de verdad de una proposición le asignamos una columna a cada proposición que interviene, sea ésta simple o compuesta, normalmente comenzando con las más simples y progresando en el orden de complejidad de las proposiciones componentes.
El número de filas de la tabla viene dado por la potencia
 , donde
, donde  es el número de proposiciones en la forma más simple que forman la proposición compuesta dada.
es el número de proposiciones en la forma más simple que forman la proposición compuesta dada.
No hay comentarios:
Publicar un comentario